Welcome to CogSci Unpacked, an exciting blog series dedicated to summarizing academic papers from the Cognitive Science, a CSS Journal. Our goal is to bridge the gap between academia and the broader public, fostering a better understanding of cognitive science and making it accessible and relatable to all. If you’re curious to dive even deeper, we invite you to explore the full academic paper.
Numbers are a vital cognitive tool, integral to the functioning of society, from the democratic practice of holding elections (counting votes) to impressive feats of engineering that require complex mathematics to achieve (Cantlon et al., 2009).
Numbers are incredibly versatile, serving different purposes depending on their context of use. For example, consider the following sentence: “Player number 23 took 2nd place by scoring 3 goals”. This sentence features nominal, ordinal, and cardinal numbers, in that order. Nominals serve as unique identifiers (e.g., communications numbers), ordinals index positions in ordered sequences (e.g., years, pages), and cardinals quantify sets (e.g., people, objects) and elements of conventional scales (e.g., dollars, miles).
The relative prevalence of these three number types in natural language had never been systematically tested until our recent research. Previous studies primarily focused on how often different numbers are used, finding that number frequency decreases with magnitude in a logarithmic fashion (Coupland, 2011; Dehaene & Mehler, 1992; Dorogovtsev et al., 2005; Jansen & Pollmann, 2001; Woodin et al., 2024). This finding supports the argument that numerical cognition itself is logarithmically scaled (Dehaene & Mehler, 1992). These studies also showed that round numbers (i.e., multiples of 10 and sometimes 5), which are often used imprecisely, are used more frequently than unround numbers, especially at higher magnitudes. This result has been linked to the idea that the approximate number system is increasingly imprecise for larger numbers (Woodin et al., 2024; see also Rinaldi & Marelli, 2020)
However, these claims were based on quantitative uses of numbers, and the data used to support such claims are likely to have included ordinal or nominal uses. Therefore, the extent to which such claims regarding numerical cognition are warranted depends on how much the number frequencies capture quantitative, cardinal uses.
In our study, recently published in Cognitive Science, we conducted the first corpus analysis investigating the relative prevalence of cardinal, ordinal, and nominal numbers in natural language. By manually annotating 3,600 concordances in the Corpus of Contemporary American English (COCA; Davies, 2008), we tested how these different number types are used in American English. Concordances, or concordance lines, are lines of text that show how words (in our case, numbers) are used in context.
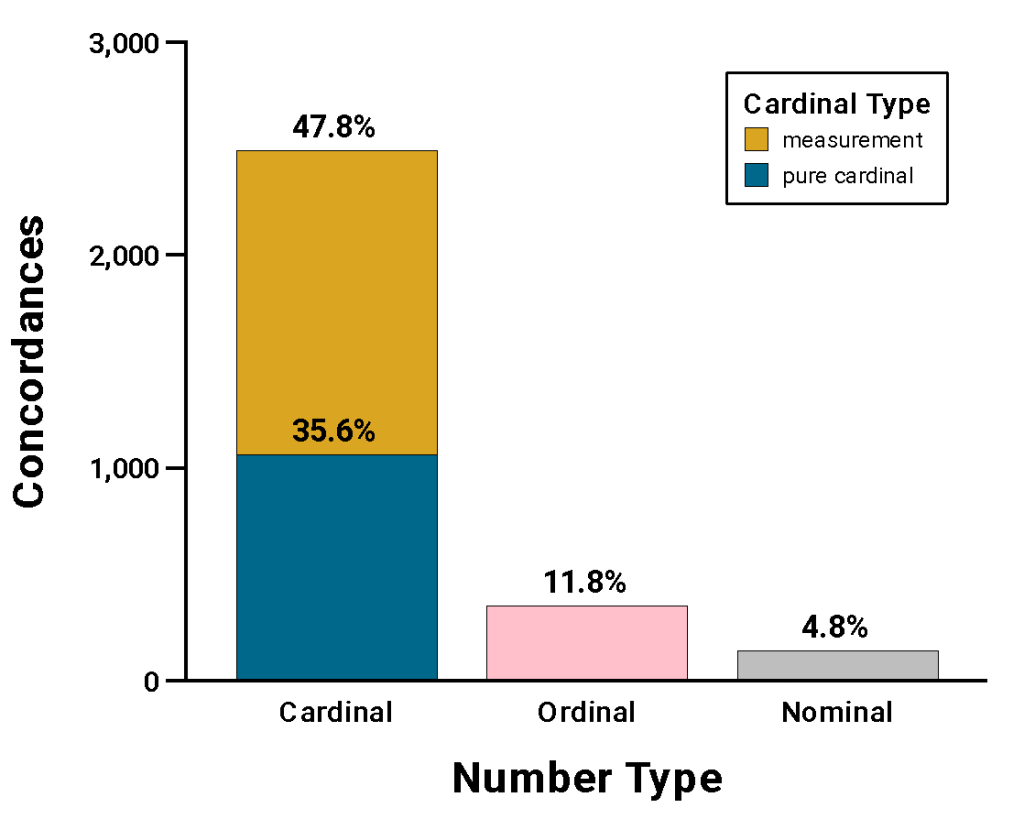
Figure 1. Counts (bars) and percentages (text) of concordances containing cardinal, ordinal, and nominal numbers, with cardinal numbers subdivided into pure cardinals and measurements.
Our results show that, in American English, cardinals are dominant, followed by ordinals, then nominals (see Fig. 1). Among quantitative uses of numbers, measurements (scales) are more common than pure cardinals (sets). Only for cardinals do round numbers (operationalized here as multiples of 5) dominate and increase with magnitude (see Fig. 2).
These results demonstrate that cardinals are the most prototypical number type, suggesting the validity of claims relating to the logarithmic nature of numerical cognition (Dehaene & Mehler, 1992), as well as the approximate number system (Woodin et al., 2024). However, nominals and especially ordinals are still relatively common, and so should be at least acknowledged when aggregating number frequencies, even when cardinals are the focal point of analyses.
Our findings are also relevant for developmental research: children tend to acquire ordinals after cardinals, and it is assumed that nominals are acquired later (e.g., Colomé & Noël, 2012; Fischer & Beckey, 1990; Miller et al., 2000). Our results raise the possibility that the order in which children acquire different number types is influenced by differential exposure to these types in adult language use. In other words, later acquisition may not necessarily entail increased cognitive difficulty.
In general, our paper uncovers a picture of numerical communication more complex and nuanced than aggregated number frequencies reveal by themselves, with language serving as an important channel via which numerical and mathematical cognition can be observed and analyzed.
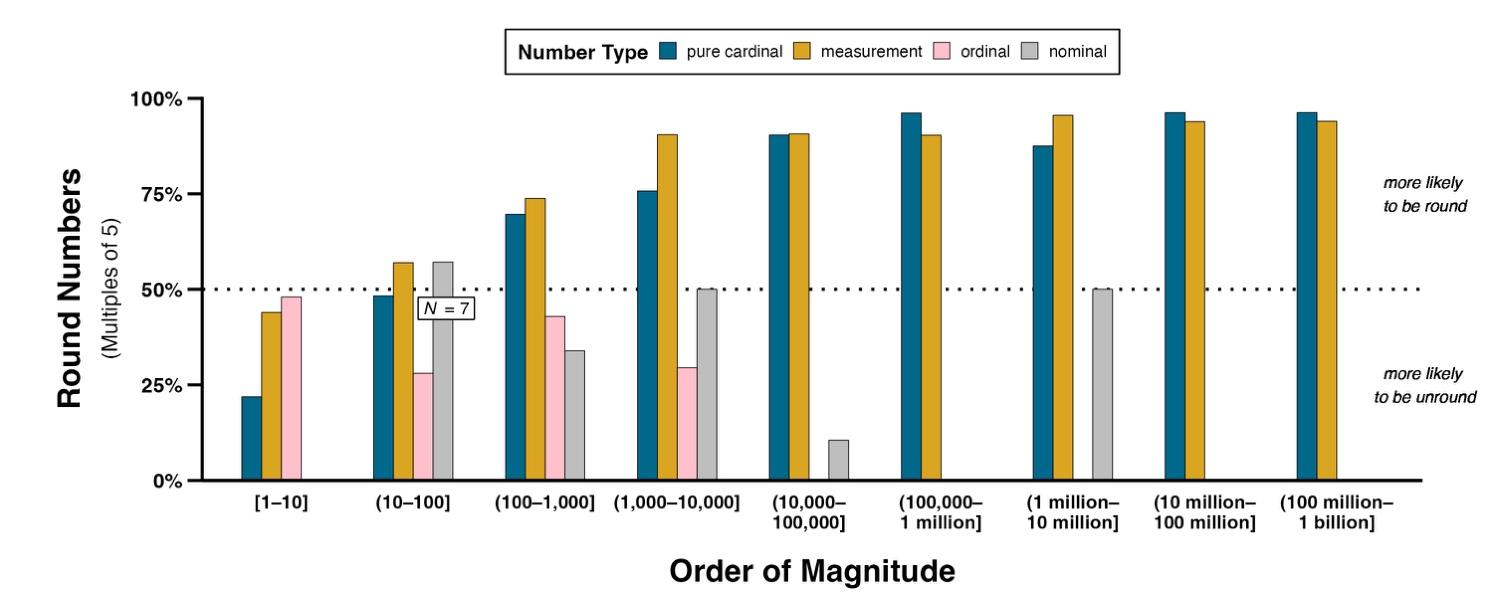
Figure 2. Percentages of concordances containing pure cardinals, measurements, ordinals, and nominals for each order of magnitude that are round (i.e., multiples of 5).
References
Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., & Pelphrey, K. A. (2009). The neural development of an abstract concept of number. Journal of Cognitive Neuroscience, 21(11), 2217. https://doi.org/10.1162/jocn.2008.21159
Colomé, À., & Noël, M.-P. (2012). One first? Acquisition of the cardinal and ordinal uses of numbers in preschoolers. Journal of Experimental Child Psychology, 113, 233–247. https://doi.org/10.1016/j.jecp.2012.03.005
Coupland, N. (2011). How frequent are numbers? Language and Communication, 31(1), Article 1. https://doi.org/10.1016/j.langcom.2010.09.001
Davies, M. (2008). The Corpus of Contemporary American English (COCA) [Computer software]. https://www.english-corpora.org/coca/
Dehaene, S., & Mehler, J. (1992). Cross-linguistic regularities in the frequency of number words. Cognition, 43(1), 1–29.
Dorogovtsev, S., Mendes, J. F., & Oliveira, J. (2005). Frequency of occurrence of numbers in the World Wide Web. Physica A: Statistical Mechanics and Its Applications, 360, 548–556. https://doi.org/10.1016/j.physa.2005.06.064
Fischer, F. E., & Beckey, R. D. (1990). Beginning kindergartners’ perception of number. Perceptual and Motor Skills, 70, 419–425. https://doi.org/10.2466/PMS.70.2.419-425
Jansen, C. J. M., & Pollmann, M. M. W. (2001). On round numbers: Pragmatic aspects of numerical expressions. Journal of Quantitative Linguistics, 8(3), 187–201. https://doi.org/10.1076/jqul.8.3.187.4095
Miller, K., Major, S. M., Shu, H., & Zhang, H. (2000). Ordinal knowledge: Number names and number concepts in Chinese and English. Canadian Journal of Experimental Psychology = Revue Canadienne De Psychologie Experimentale, 54(2), 129–140. https://doi.org/10.1037/h0087335
Rinaldi, L., & Marelli, M. (2020). The use of number words in natural language obeys Weber’s law. Journal of Experimental Psychology: General, 149(7), 1215–1230. https://doi.org/10.1037/xge0000715
Woodin, G., Winter, B., Littlemore, J., Perlman, M., & Grieve, J. (2024). Large-scale patterns of number use in spoken and written English. Corpus Linguistics and Linguistic Theory, 20(1), 123–152. https://doi.org/10.1515/cllt-2022-0082





